This website is meant as a useful resource for those interested in networks in archaeology. The current page includes tutorials to learn network science from scratch, but also a list of network science software and a glossary. The bibliography page includes a complete bibliography of all published archaeological network research.
Network Analysis with Visone Tutorial
Network visualisation with The Vistorian
Network science and statistical techniques for dealing with uncertainties in archaeological datasets
Network Science with Netlogo Tutorial
Importing a Roman transport network with Netlogo
Network structures and assembling code in Netlogo
Network Analysis with Cytoscape Tutorial
Network Science Software
Network Science Glossary
External Resources
Network Analysis with Visone Tutorial
This tutorial is a step-by-step guide to network creation, visualisation and analysis using the free to use software Visone, through an archaeological case study on Maya obsidian networks in Mesoamerica.
Download the tutorial files as a .zip archive
Please cite this tutorial as:
Weidele, D., and Brughmans, T. (2015) Network Analysis with Visone Tutorial. https://archaeologicalnetworks.wordpress.com/resources/#Visone
The archaeological case study and data used here is published as (we thank the authors of this paper for allowing us to use this study as an example and for providing feedback on the tutorial):
Golitko, M., Meierhoff, J., Feinman, G. M., & Williams, P. R. (2012). Complexities of collapse : the evidence of Maya obsidian as revealed by social network graphical analysis. Antiquity, 86: 507–23.
Network visualisation with The Vistorian
This tutorial teaches you how to upload network data to The Vistorian online and how to explore its different visualisation features. The Vistorian is a free-to-use online service developed by Benjamin Bach.
Download the tutorial PDF and data files here (open the dataset .xls files in Excel and save them as .csv files):
Please cite this tutorial as:
Brughmans, T. and Bach, B. (2018) The Vistorian: exploring archaeological networks. https://archaeologicalnetworks.wordpress.com/resources/#vistorian
The archaeological data used in this tutorial is the ICRATES database of tablewares in the Roman East. To cite this data use the following reference:
Bes, P., 2015. Once upon a Time in the East. The Chronological and Geographical Distribution of Terra Sigillata and Red Slip Ware in the Roman East. Roman and Late Antique Mediterranean Pottery 6. Archaeopress, Oxford.
Network science and statistical techniques for dealing with uncertainties in archaeological datasets
This tutorial created by Matt Peeples provides an overview of applying statistical techniques in R to perform sensitivity analyses of network metric results in the context of uncertainties in archaeological datasets. This tutorial requires basic knowledge of network science and R.
Please cite this tutorial as:
Peeples, M. A. (2017). Network Science and Statistical Techniques for Dealing with Uncertainties in Archaeological Datasets. [online]. Available: http://www.mattpeeples.net/netstats.html
Network Science with Netlogo Tutorial
This tutorial provides an introduction to creating agent-based network models with Netlogo. By working through this tutorial you will learn how to create nodes, create edges, perform layouts introduce probability in edge creation, create a trade process working on the network and how to derive network measures.
Download the tutorial as a .pdf file
Please cite this tutorial as:
Brughmans, T. (2016). Network Science with Netlogo Tutorial, https://archaeologicalnetworks.wordpress.com/resources/#netlogo
Importing a Roman Transport network with Netlogo
This tutorial provides an introduction to downloading open Roman datasets via https://projectMERCURY.eu and importing them into a Netlogo model. We will use the ORBIS dataset (http://orbis.stanford.edu/) to create a set of Roman settlements and major routes between them.
Download tutorial as a .pdf file
Input data:
– ‘orbis.graphml’(click download, the input data file is included in the folder ‘data’)
Please cite this tutorial as:
Brughmans, T. (2018). Importing a Roman Transport network with Netlogo, Tutorial, https://archaeologicalnetworks.wordpress.com/resources/#transport .
Network structures and assembling code in Netlogo
An introduction to assembling Netlogo code from different sources to create a complex archaeological model in a modular fashion. It uses as input a Netlogo model creating different network structures, a Netlogo model creating a Roman transport network, and a dataset representing a Roman transport network.
Download tutorial as a .pdf file.
Input data:
– Network structures model.
– Transport network model and data.
Please cite this tutorial as:
Brughmans, T. (2018). Network structures and assembling code in Netlogo, Tutorial, https://archaeologicalnetworks.wordpress.com/resources/#structures .
Network Analysis with Cytoscape Tutorial
This tutorial is a step-by-step guide to network creation, visualisation and analysis using the free to use software Cytoscape, through an archaeological and geographical case study on inter-visibility in Iron Age and Roman Southern Spain.
Files:
Download the tutorial in PDF format
Download the network spreadsheet
Download the network attributes spreadsheet
Please cite this tutorial as:
Brughmans, T. (2013). Network Analysis with Cytoscape Tutorial, November 2013. https://archaeologicalnetworks.wordpress.com/resources/#cytoscape
The archaeological case study and data used here is published as:
Brughmans, T., Keay, S., & Earl, G. (2015). Understanding Inter-settlement Visibility in Iron Age and Roman Southern Spain with Exponential Random Graph Models for Visibility Networks. Journal of Archaeological Method and Theory, 22: 58–143. DOI: 10.1007/s10816-014-9231-x
Brughmans, T., Keay, S., & Earl, G. P. (2014). Introducing exponential random graph models for visibility networks. Journal of Archaeological Science, 49: 442–54. DOI: 10.1016/j.jas.2014.05.027
Network Science software
Pajek
Up to date set of analysis techniques, can handle large networks, good manual and supporting documentation, less easy to use than UCINET, includes some specific features not included in UCINET (Triad counts; nice matrix graphs; graphs automatically separating components).
UCINET
up to date set of analysis techniques, good supporting documentation, great for converting to different network data formats. See handout network analysis practical 2.
Cytoscape
Poor documentation, user-friendly interface, easy analysis. See handout network analysis practical 1.
Gephi
Verry pretty visualisation, poor documentation, user-friendly interface, manual modification of layout algorithm settings.
GIS
Grass and ArcGIS (networkAnalyzer) have some network features. Can be used to produce visibility networks, least-cost paths, etc.
Processing
visualization and animation, programming skills needed.
Mathematica
Tools in the Wolfram language for analysing, modelling and visualising networks.
See also this iGraph interface for Mathematica.
Matlab: http://www.levmuchnik.net/Content/Networks/ComplexNetworksPackage.html
R Language
You can do basically anything you want if you can be bothered to code it, some great network analysis libraries (network, sna, Rnetworks, igraph, ergm, networkDynamic, Rsiena, statnet, tnet).
Excel and NodeXL
Everyone knows how Excel works, now you can use it to make networks.
TRACER
A text re-use tracing software
VISONE
Many functions and also runs RSiena
Blocks
free separate program for blockmodeling – very good at it, does nothing else. Result pages somewhat cumbersome, but very good documentation
Network Science Glossary
Introduction
This glossary contains definitions of concepts commonly used in network science. For each concept we first provide a formal definition, often followed by a description of the main use of the concept or its implications. The networks represented in the figures accompanying this glossary are used to illustrate a number of concepts. Where examples drawn from figures are provided, we refer to connected nodes by their number separated by a hyphen (e.g. 1-2 indicates that node 1 is connected to node 2). A key reference work for most of the concepts described here is that by Wasserman and Faust (1994), in which more elaborate descriptions, mathematical formulations, and additional bibliographic resources can be found. A limited number of additional primary sources are given in this glossary and included in a separate bibliography below. The terms included in this glossary are underlined.
Acknowledgements
The glossary presented here benefited greatly from discussions with members of the algorithmics group at the Department of Computer and Information Science of the University of Konstanz, John M. Roberts Jr., and the contributors to the special issue of Journal of Archaeological Method and Theory where it was first published. It is co-authored with Habiba. The authors of this paper are solely responsible for any remaining mistakes in this glossary.
Citation
Please refer to this glossary by citing the paper where it originally appeared:
Collar, A., Coward, F., Brughmans, T., & Mills, B. J. (2015). Networks in Archaeology: Phenomena, Abstraction, Representation. Journal of Archaeological Method and Theory, 22, 1–32. doi:10.1007/s10816-014-9235-6
Glossary
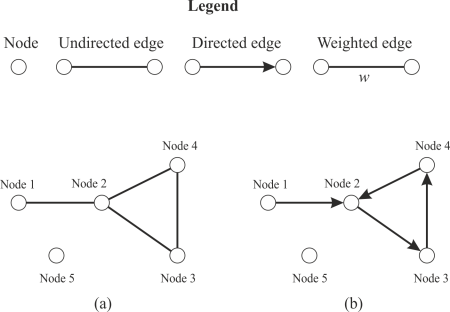
Actor: See node.
Acyclic network: Defined as a directed network with no cycles.
For example, the directed network in figure 1b is not acyclic because it includes the cycle 2-3-4-2. Examples of acyclic networks include citation networks and dendrograms.
Adjacency matrix: Defined as a way of representing a network where there is a row and a column for each node, and the values in the cells indicate whether an edge exists between a pair of nodes.
Affiliation network: See two-mode network.
Arc: See directed edge.
Average degree: See degree.
Average shortest path: See geodesic.
Betweenness centrality: A node’s betweenness centrality is defined as the fraction of the number of geodesics passing through this node over the number of geodesics between all pairs of nodes in the network.
Nodes with a high betweenness centrality are often considered to be important intermediaries for controlling the flow of resources between other nodes, because they are located on paths between many other node pairs. The concept of brokerage is often mentioned in relation to betweenness centrality. Nodes which are incident to the only edge connecting two subsets of nodes in the network are in a position to broker the relationship between these nodes. These nodes will typically have a high betweenness centrality but not necessarily a high degree or closeness centrality. Betweenness centrality was first quantitatively expressed by Anthonisse (1971) and Freeman (1977).
Bipartite network: See two-mode networks.
Blockmodel: Defined as a partitioning into blocks of structurally equivalent nodes, where the blocks are connected by hypothesised edges.
In blockmodelling the rows and columns of adjacency matrices are arranged so that structurally equivalent nodes are in adjacent positions in the matrix, and the edges between different blocks can be studied. First introduced by White, Boorman, and Breiger (1976).
Brokerage: see betweenness centrality.
Centrality: Defined as a family of measures of the node’s position within the network, which represent a ranking of nodes (see betweenness, closeness, degree, and eigenvector centralities).
Centrality measures are used to identify the most important or prominent nodes in the network, depending on the different definitions of importance or prominence implemented in the network measure used.
Clique: A clique is a subset of nodes in a network, where every pair of nodes is connected by an edge.
In the social sciences only cliques of three nodes or more are usually considered. For example, in figure 1a nodes 2, 3, 4 form a clique of size 3. The definition of a clique is independent of whether it applies to the whole network or not. For example, a network can consist of multiple cliques, or an entire network can be one clique. The latter can also be called a complete network.
Closeness centrality: The closeness centrality of a node is defined as the inverse of the sum of the geodesics of that node to all other nodes divided by the number of nodes in the network.
The closeness centrality of a node gives an indication of how close this node is to all other nodes in the network, represented as the number of steps in the network that are necessary on average to reach another node. Nodes with a high closeness centrality score could be considered important or prominent, since they can share and obtain resources in less steps than other nodes. Early quantitative implementations of closeness centrality are reviewed by Freeman (1979).
Clustering coefficient: Defined as the number of closed triplets over the total number of triplets in a network, where a triplet is a set of three nodes with two (open triplet) or three (closed triplet) undirected edges between them.
The clustering coefficient represents the average probability that two nodes connected to a third node are themselves connected, and it is commonly used for this purpose since the publication of the ‘small-world’ network model (Watts and Strogatz 1998). The clustering coefficient of a network is closely related to the concept of transitivity in the social sciences, which captures the notion that “a friend of a friend is a friend”. Transitivity refers to the tendency of an open triplet to become a closed triplet.
Cohesion: See density.
Complete network: See clique.
Connected component: Defined as a subset of an undirected network in which any pair of nodes can be connected to each other via at least one path, and where there can be no paths to any nodes outside this subset.
For example, in the undirected network in figure 5a there are two connected components: node 5, and nodes 1, 2, 3, 4.
Connection: See edge.
Cycle: Defined as a path in a directed network in which the starting node and ending node are the same. It is also called a closed path.
For example, in figure 1b the path 2-3-4-2 is a cycle. See also acyclic network.
Degree: The degree of a node is defined as the number of edges incident to this node.
The average degree of a network is the sum of the degrees of all nodes in this network divided by the number of nodes. In a directed network, the indegree of a node refers to the number of incoming incident edges of a node. In a directed network, the outdegree of a node refers to the number of outgoing incident edges of a node. For example, node 2 in figure 1a has a degree of 3, whilst in figure 1b the same node can be said to have an indegree of 2 and an outdegree of 1.
Degree centrality: Defined as the centrality of a node based on the number of edges incident to this node.
According to the degree centrality measure, a node is important or prominent if it has edges to a high number of other nodes.
Degree distribution: Defined as the probability distribution of all degrees over the whole network.
The measure is commonly used to compare the structure of networks since the publication of the ‘scale-free’ network structure (Albert & Barabási 2002, p. 49; Barabási & Albert 1999; Newman 2010, p. 243-247). In ‘scale-free’ networks the degree distribution follows a power-law.
Density: Defined as the fraction of the number of edges that are present to the maximum possible number of edges in the network.
Cohesion is a commonly used concept which is often operationalised using the density measure. For other cohesion measures see Wasserman and Faust (1994, 249-290).
Diameter: Defined as the length of the longest geodesic in the network.
Directed edge: Defined as an ordered pair of nodes, which is often graphically represented as an arrow drawn from a starting node to an end node.
A directed edge is asymmetric. It connects a starting node with an ending node, and cannot be traversed in the other direction. For example, all edges in figure 1b are directed edges.
Directed network: Defined as a set of nodes and a set of directed edges.
A path through a directed network will need to follow the direction of the directed edges. For example, the network in figure 1b is a directed network.
Distance: See path length.
Dyad: Defined as any pair of nodes in a network that may or may not have an edge between them.
For undirected edges there are two possible dyadic relationships: connected, or not connected. For directed edges, there are four: unconnected; connected in one direction; connected in the other direction; connected in both directions.
Edge: Defined as a line between a pair of nodes, representing some kind of relationship between them.
Many synonyms exist to refer to an edge, including tie, arc, relationship, link, connection and line. An edge can be directed or undirected, and weighted or unweighted. The concept ‘arc’ is often used to refer to a directed edge.
Ego-network: Defined as a network consisting of a node (called ego), the nodes it is directly connected to, and the edges between these nodes.
Eigenvector centrality: The eigenvector centrality of a node is defined in terms of the eigenvector centrality of nodes incident on it.
More descriptively, instead of assigning a single centrality score to a node, a node’s eigenvector centrality is defined in terms proportional to the nodes incident on it. A node with a high eigenvector centrality is a node that is connected to other nodes with a high eigenvector centrality. See Newman (2010, 169-172) for the procedure to calculate eigenvector centrality.
Embeddedness: A polyvalent concept that comprises two variants. The first is the structural integration of a node or any group of nodes within the network. Different measures for structural integration exist. The E/I index is one example of this, which is calculated as a ratio of the number of edges within a group of nodes (internal) and between groups of nodes (external). The second variant, as popularized in economic theory through the work of Polanyi (1944) and Granovetter (1985), relates to the intertwined nature of social, economic, political, religious, and cultural interactions. See Borck et al. (this issue) and Hess (2004) for overviews of this concept.
Equivalence: See structural equivalence.
Geodesic: Defined as the path between a pair of nodes with the shortest path length.
Sometimes referred to as the shortest path length between a pair of nodes. For example, the geodesic between nodes 1 and 3 in figure 1b is the path 1-3 with a length of 1. The average shortest path length is the average of all geodesics in a network.
Graph: See network.
Heterophily: Defined as a tendency of nodes to become connected to other nodes that are dissimilar under a certain definition of dissimilarity.
For example, in figure 2a a node with an attribute value represented in grey will have a tendency of being connected to a node with a different attribute value represented in white.
Homophily: Defined as a tendency of nodes to become connected to other nodes that are similar under a certain definition of similarity.
For example, in figure 2b a node with an attribute value represented in grey will have a tendency of being connected to a node with the same attribute value.
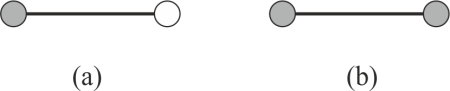
Indegree: See degree.
Isolates: Defined as nodes in a network which have no incident edges.
For example, node 5 in figure 1a is an isolate.
Line: See edge.
Link: See edge.
Network: Defined as a set of nodes and a set of edges.
In mathematics a network is referred to as a graph, whilst in the social sciences networks often consist of social nodes and edges, and are referred to as social networks.
Node: Defined as an atomic discrete entity representing a network concept.
A vertex (plural vertices) is a commonly used synonym to refer to a node. The term actor is sometimes used as a synonym for nodes in the social sciences.
One-mode network: See two-mode network.
Outdegree: See degree.
Path: Defined as a walk between a pair of nodes in which no nodes and edges are repeated.
For example, nodes 1 and 3 in figure 1b are connected by the path 1-2-3.
Path length: Defined as the number of edges in a path.
For example, nodes 1 and 3 in figure 1b are connected by the path 1-2-3, which has a path length of 2.
Power-law: Defined as a mathematical relationship between two entities where the frequency of one entity varies as a power of the second entity. More formally, the probability of a node with degree k is proportional to ka.
Commonly used to describe the degree distribution of networks with a ‘scale-free’ structure (Barabási & Albert 1999). When a network’s degree distribution follows a power-law, it implies that few nodes have a much higher degree than all other nodes in the network and most nodes have a very low degree. Nodes with a very high degree, sometimes referred to as “hubs” in the network, significantly reduce the average shortest path length of the network.
Relationship: See edge.
Shortest path: See geodesic.
‘Small-world’ network: A ‘small-world’ network is defined as a network in which the average shortest path length is almost as small as that of a uniformly random network with the same number of nodes and density, whereas the clustering coefficient is much higher than in a uniformly random network (a uniformly random network is defined as a network in which each edge exists with a fixed probability p).
The ‘small-world’ network structure as described here was first published by Watts and Strogatz (1998). This structure illustrates that relatively few edges between clusters of nodes are needed to significantly reduce the average shortest path length. It implies that resources can flow between any pairs of nodes in the network relatively efficiently, whilst maintaining a high degree of clustering.
Social network: See network.
Strongly connected component: Defined as a connected component in a directed network.
In a directed network a connected component is always either strongly or weakly connected. For example, in figure 1b node 5 is a connected component, whilst the set of nodes 1, 2, 3, and 4 are not because node 1 cannot be reached by a path from the other nodes.
Strong tie: A number of theoretical network models used in the social sciences rely on a distinction between strong and weak ties (particularly those drawing on Granovetter 1973). The distinctions between the two, however, are rarely formally defined. In general, strong ties are used to describe frequently activated relationships (such as family/kin ties) whereas weak ties are used to describe infrequently accessed connections (acquaintances). Strong ties tend to be among actors with similar sets of overlapping relationships whereas weak ties more often connect sets of actors who would otherwise be unconnected. In weighted networks, thresholds on the distribution of weights across a network as a whole are often used to define strong vs. weak ties though there are no consistent rules used for this distinction.
Structural equivalence: Defined as, two nodes are structurally equivalent if they have identical edges to and from all other nodes in the network (see Lorrain and White 1971).
Structural equivalence is used to identify nodes which have the same position in a network. It can be used to inform blockmodelling. In the social sciences, the structural similarities identified through structural equivalence are used to study social positions and social roles.
Tie: see edge.
Transitivity: see clustering coefficient.
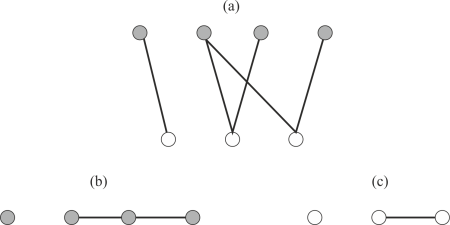
Two-mode network: Defined as a network in which two sets of nodes are defined as modes. In a two-mode network, nodes of one mode can only be connected to nodes of another node.
Two-mode networks are sometimes referred to as bipartite networks. The definition of modes depends on the research context. In the social sciences two-mode networks are often used as a representation of affiliation networks, where one mode represents individuals and the other mode represents institutions or other concepts these individuals are affiliated with (given the definition of affiliation within the research context). For example, individuals may be affiliated to political parties, or be members on different boards of directors. The most common example of the use of two-mode networks in archaeology is to represent sites as one mode and the artefact types found on sites as a second mode. Two-mode networks can be transformed into two different one-mode networks by focusing on either one of the two modes. In a one-mode network, only the nodes of one of the two modes is included, and pairs of nodes are connected by an edge if both have a connection to at least one node of the other mode in the two-mode network. For example, the two-mode network in figure 3a (where two different modes are represented as nodes with a different colour) can be transformed into a one-mode network of only grey nodes (Fig. 3b) or a one-mode network of only white nodes (Fig. 3c).
Undirected edge: Defined as an unordered pair of nodes, which is often graphically represented as a line drawn between the pair of nodes.
An undirected edge is symmetric. Typically just called an edge. For example, all edges in figure 1a are undirected edges.
Undirected network: a set of nodes and a set of undirected edges.
An undirected network is symmetric. For example, the network in figure 1a is an undirected network.
Unweighted edge: Defined as an edge which is not weighted.
Typically just called an edge. See also weighted edge.
Unweighted network: Defined as a set of nodes and a set of unweighted edges.
Valued network: See weighted network.
Vertex: See node.
Walk: A walk between a pair of nodes is defined as any sequence of nodes connected through edges which has that pair of nodes as endpoints.
In contrast to a path, nodes and edges can be repeated in a walk. For example, in figure 1b a walk between nodes 2 and 3 could be 2-3-4-2-3.
Weakly connected component: Defined as a connected component in a directed network where the directionality of edges is ignored.
In a directed network a connected component is always either strongly or weakly connected. For example, in figure 1b there are two weakly connected components: node 5, and nodes 1, 2, 3, 4.
Weak tie: See strong tie.
Weighted edge: Defined as an edge with a value associated to it.
These values are often real numbers but they can also be any concept connecting the end nodes of the edge. The definition of an edge weight depends on the research context. Weights could be represented as an attribute of an edge. Thresholding can be applied to select a subset of edges with a given edge weight.
Weighted network: Defined as a set of nodes and a set of weighted edges.
References cited in glossary
Albert, R., & Barabási, A. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics, 74(January), 47–97.
Anthonisse, J. M. (1971). The Rush in a graph. Amsterdam: Mathematische Centrum.
Barabási, A.-L., & Albert, R. (1999). Emergence of Scaling in Random Networks. Science, 286/5439: 509–12. DOI: 10.1126/science.286.5439.509
Borck, L., Mills, B. J., Peeples, M. A., & Clark, J. J. (this issue). Are Social Networks Survival Networks? An Example from the Late Prehispanic U.S. Southwest. Journal of Archaeological Method and Theory.
Freeman, L. C. (1977). A Set of Measures of Centrality Based on Betweenness. Sociometry, 40/1: 35–41.
Freeman, L. C. (1979). Centrality in Social Networks. I. Conceptual Clarification. Social networks, 1: 215–39.
Granovetter, M. (1973). The strength of weak ties. American Journal of Sociology 78(6): 1360–1380.
Granovetter, M. (1985). Economic action and social structure: The problem of embeddedness. The American Journal of Sociology, 91(3), 481–510.
Hess, M. (2004). “Spatial” relationships? Towards a reconceptualization of embeddedness. Progress in Human Geography, 28(2), 165–186.
Lorrain, F., & White, H. C. (1971). Structural equivalence of individuals in social networks. Journal of mathematical sociology1, 1: 49–80.
Newman, M. E. J. (2010). Networks: An introduction. Oxford: Oxford University Press.
Polanyi, K. (1944) The great transformation. The political and economic origins of our time. Boston: Beacon Press.
Wasserman, S., & Faust, K. (1994). Social network analysis: methods and applications. Cambridge: Cambridge University Press.
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393(6684), 440–2. doi:10.1038/30918
White, H. C., Boorman, S. A., & Breiger, R. L. (1976). Social structure from multiple networks. I. Blockmodels of roles and positions. American Journal of Sociology, 81/4: 730–79.
External resources
There are some great resources available on other websites, definitely check out the following:
Tutorials
First steps on Historical Network Research
Agent-based modelling tutorials on Simulating Complexity
Software
Tools list on Historical Network Research
Resources list on Netplexity
Related projects and blogs
Electric Archaeology
Hestia Project
Historical Network Research
Netplexity
Réseaux et Histoire
Simulating Complexity
Six Degrees of Spaghetti Monsters
Recorded presentations from the Historical Network Research events.